Authors:
(1) Agustin Moreno;
(2) Francesco Ruscelli.
Table of Links
- Abstract
- Introduction
- Preliminaries
- The B-signature
- GIT sequence: low dimensions
- GIT sequence: arbitrary dimension
- Appendix A. Stability, the Krein–Moser theorem, and refinements and References
Appendix A. Stability, the Krein–Moser theorem, and refinements
Now we explain how the GIT sequence topologically encodes the (linear) stability of periodic orbits, and compare it to the basic notions of Krein theory, and the Krein–Moser stability theorem. We will also explain how to obtain Theorem A.
We follow the exposition in Ekeland’s book [Eke90] (see also [Ab01]). Consider a linear symplectic ODE

One can show that the ODE x˙ = JA(t)x is (strongly) stable if and only if R(T) is (strongly) stable [Eke90]. Moreover, stability is equivalent to R(T) being diagonalizable (i.e. all eigenvalues are semi-simple), with its spectrum lying in the unit circle [Eke90].
Now, consider an elliptic pair {λ, λ} of eigenvalues of a symplectic matrix R. Then any other symplectic matrix close to R will also have simple eigenvalues in the unit circle different from ±1 (otherwise an eigenvalue would have to bifurcate into two, as every eigenvalue comes in quadruples, which is not possible if eigenspaces are 1-dimensional). Therefore in this situation, R is strongly stable. The case of eigenvalues with higher multiplicity is dealt with via Krein theory. Whenever two elliptic eigenvalues come together, this gives a criterion for when they cannot possibly escape the circle and transition into a complex quadruple. This works as follows.
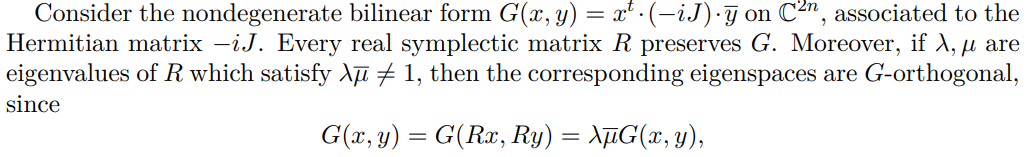
if x, y are the corresponding eigenvectors. Moreover, if we consider the generalized eigenspaces

Definition A.2. (Krein-positivity/negativity) If λ is an eigenvalue of the symplectic matrix R with |λ| = 1, then the signature (p, q) of Gλ is called the Krein-type or Krein signature of λ. If q = 0, i.e. Gλ is positive definite, λ is said to be Krein-positive. If p = 0, i.e. Gλ is negative definite, λ is said to be Krein-negative. If λ is either Krein-negative or Krein-positive, we say that it is Krein-definite. Otherwise, we say that it is Krein-indefinite.
If λ is of Krein-type (p, q), then λ is of Krein-type (q, p) [Eke90]. If λ satisfies |λ| = 1 and it is not semi-simple, then it is easy to show that it is Krein-indefinite [Eke90]. Moreover, ±1 are always Krein-indefinite if they are eigenvalues, as they have real eigenvectors x, which are therefore G-isotropic, i.e. G(x, x) = 0. The following, originally proved by Krein in [Kre1; Kre2; Kre3; Kre4] and independently rediscovered by Moser in [M78], gives a characterization of strong stability in terms of Krein theory:
Theorem 3 (Krein–Moser). R is strongly stable if and only if it is stable and all its eigenvalues are Krein-definite.
See [Eke90] for a proof. Note that this generalizes the case where all eigenvalues are simple, different from ±1 and in the unit circle, as discussed above. Now, the way that the GIT sequence ties up with Krein theory is the following.
Proposition A.1 ([FM]). For a Wonenburger matrix, the Krein signature coincides with the B-signature, for elliptic eigenvalues.
Example A.3. As a simple example, to illustrate Proposition A.1, consider the Wonenburger matrices
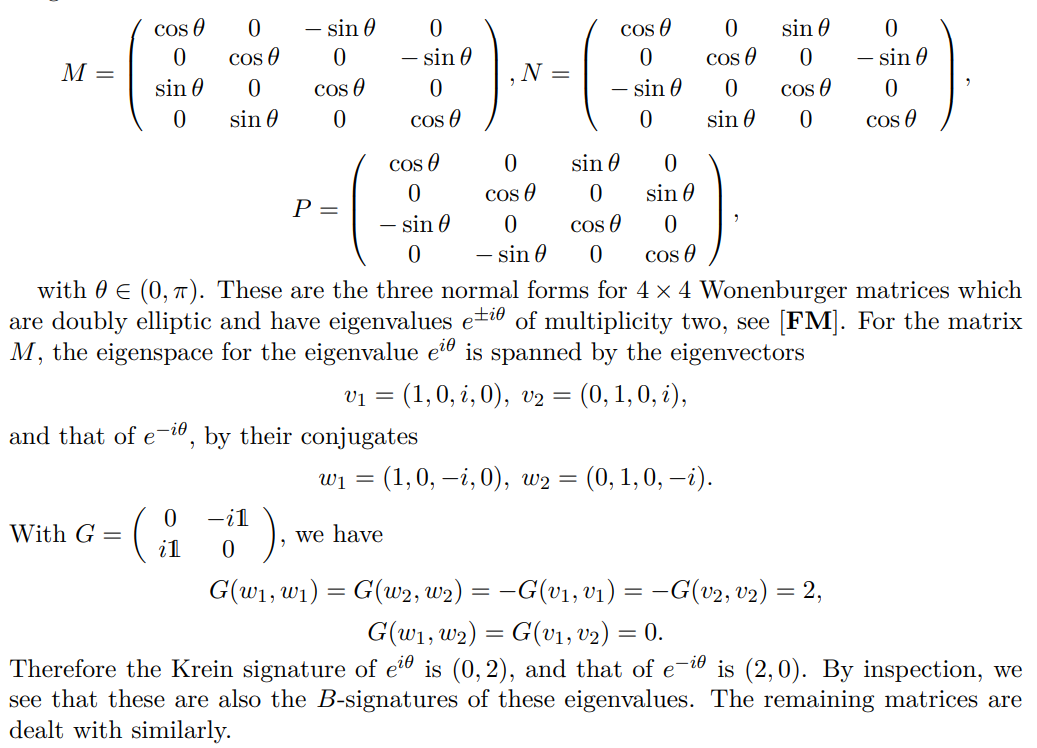
As a corollary of the Krein–Moser theorem and of Proposition A.1, we obtain the following.
Theorem 4. Let R be a Wonenburger matrix. Then R is strongly stable if and only if it is stable and all its eigenvalues are B-definite.

In higher dimensions, whether or not a given high-multiplicity elliptic or hyperbolic eigenvalue of a Wonenburger matrix can be perturbed to be a complex quadruple is determined by whether or not its B-signature is definite; see e.g. Figure 9 and Remark 5.2. This gives a topological proof of the Krein–Moser theorem in all dimensions, and in fact generalizes it for the hyperbolic case, in the case of Wonenburger matrices, proving Theorem A in the Introduction.
References
[Ab01] Abbondandolo, Alberto. Morse theory for Hamiltonian systems. Chapman & Hall/CRC Research Notes in Mathematics, 425. Chapman & Hall/CRC, Boca Raton, FL, 2001. xii+189 pp. ISBN: 1-58488- 202-6
[Ay22] Aydin, Cengiz. From Babylonian lunar observations to Floquet multipliers and Conley-Zehnder Indices. Preprint arXiv:2206.07803, 2022.
[AFKM] Aydin, Cengiz; Frauenfelder, Urs; Koh, Dayung; Moreno, Agustin. Symplectic methods in space mission design. Proceedings of the 2023 AAS/AIAA Astrodynamics Specialist Conference, 2023.
[Br69] Broucke, R. Stability of periodic orbits in the elliptic, restricted three-body problem. AIAA J. 7,1003 (1969).
[Eke90] Ekeland, Ivar. Convexity methods in Hamiltonian mechanics. Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 19. Springer-Verlag, Berlin, 1990. x+247 pp. ISBN: 3-540-50613-6
[FM] Frauenfelder, Urs; Moreno, Agustin. On GIT quotients of the symplectic group, stability and bifurcations of periodic orbits, Journal of Symplectic Geometry. To appear.
[FMb] Frauenfelder, Urs; Moreno, Agustin. On doubly symmetric periodic orbits. Celestial Mechanics & Dynamical Astronomy, 135 (2023), no. 2, Paper No. 20.
[HD98] Howard, James E.; Dullin, Holger R. Linear stability of natural symplectic maps. Phys. Lett. A 246 (1998), no. 3-4, 273–283.
[HM87] Howard, J. E.; MacKay, R. S. Calculation of linear stability boundaries for equilibria of Hamiltonian systems. Phys. Lett. A 122 (1987), no. 6-7, 331–334.
Kre1] Krein, M.: Generalization of certain investigations of A.M. Liapunov on linear differential equations with periodic coefficients. Doklady Akad. Nauk USSR 73 (1950) 445-448.
Kre2] Krein, M.: On the application of an algebraic proposition in the theory of monodromy matrices. Uspekhi Math. Nauk 6 (1951) 171-177.
[Kre3] Krein, M.: On the theory of entire matrix-functions of exponential type. Ukrainian Math. Journal 3 (1951) 164-173.
[Kre4] Krein, M.: On some maximum and minimum problems for characteristic numbers and Liapunov stability zones. Prikl. Math. Mekh. 15 (1951) 323-348.
[M78] Moser, Jürgen. A fixed point theorem in symplectic geometry. Acta Math. 141 (1978), no. 1-2, 17–34.
(A. Moreno) Universität Heidelberg, Mathematisches Institut, Heidelberg, Germany Email address: agustin.moreno2191@gmail.com
(F. Ruscelli) Universität Heidelberg, Mathematisches Institut, Heidelberg, Germany Email address: fruscelli@mathi.uni-heidelberg.de
This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.