Authors:
(1) Wahei Hara;
(2) Yuki Hirano.
Table of Links
- Abstract and Intro
- Exchanges and Mutations of modifying modules
- Quasi-symmetric representation and GIT quotient
- Main results
- Applications to Calabi-Yau complete intersections
- Appendix A. Matrix factorizations
- Appendix B. List of Notation
- References
5. Applications to Calabi-Yau complete intersections

Therefore, (5.A) and (5.B) gives an equivalence

Proposition 5.1. The restriction of (5.F
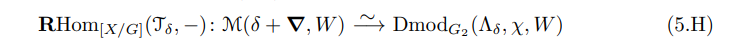
to a magic window and the functor (5.G)
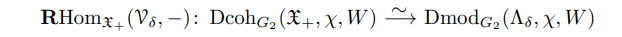
are equivalences.

Since the bottom functor is an equivalence by Theorem A.5, so is (5.G).

for derived factorization categories is an equivalence by Theorem A.5.
The following shows that the equivalences of magic windows generating the group action (5.D) correspond to mutation functors between noncommutative matrix factorizations.

Proof. We only show that the left square commutes, since the commutativity of the right one follows from a similar argument. Consider the following diagram

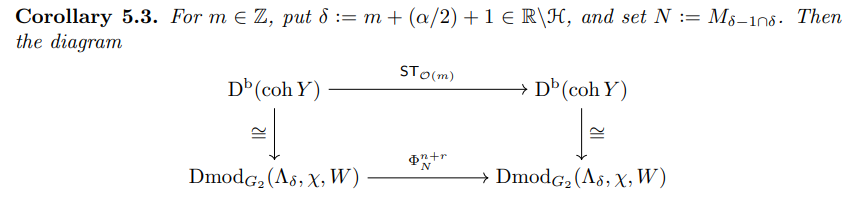
commutes, where the vertical equivalences are the compositions of (5.C) and (5.H).


Lemma 5.5. There is an isomorphism

where the first isomorphism follows from Lemma A.6. This finishes the proof.
The following is a generalization of [KO, Theorem 8.5], which we prove by a similar argument as in loc. cit.
Lemma 5.6. The following diagram commutes.
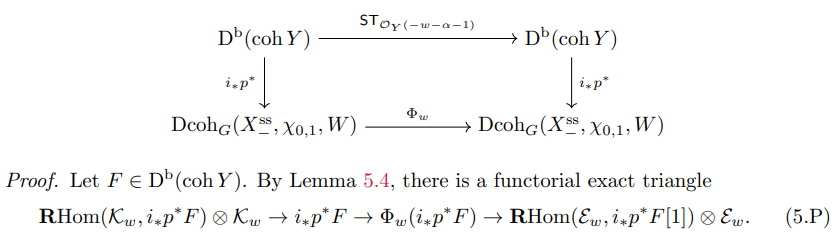
Thus it is enough to show that there is a natural isomorphism
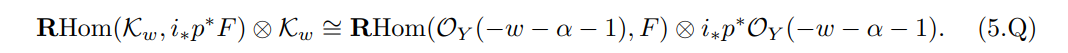
By Lemma 5.6, there is an isomorphism

Proof of Corollary 5.3. For simplicity, write


Therefore, the assertion follows from Theorem 5.2.
This paper is available on arxiv under CC0 1.0 DEED license.
[1] Although [HSh] only discusses complexes, there are similar functors and semi-orthogonal decompositions for matrix factorizations by [BFK2], and so a similar argument as in [HSh] works in our setting.
