Authors:
(1) Scott Conn, California Institute of Technology, Pasadena, California;
(2) Joseph Fitzgerald, California Institute of Technology, Pasadena, California;
(3) Jorn Callies, California Institute of Technology, Pasadena, California.
Table of Links
3. Models
a. The PM Model

For each event, we use a constant mixed layer depth that is an average of the time-varying mixed layer depth over duration of the event. Since the events are relatively short, the error in this approximation is minimal for most events. We make this choice of a constant mixed layer depth to avoid complications that arise otherwise, especially in the YBJ model discussed below.


b. The YBJ Model
The YBJ equation is a three-dimensional partial differential equation, making it substantially more computationally expensive to integrate than the PM model. We solve the YBJ equation using the pseudospectral solver Dedalus (Burns et al. 2020) with a mixed explicit and implicit diagonal RK2 scheme. As discussed above, we start the simulations with no waves.
We use a domain that is 400 km×400 km in the horizontal (centered on the mooring array) and 4 km deep. Each dimension is discretized with 128 modes. The vertical dimension is finite and represented using Chebyshev polynomials. The horizontal dimensions are made periodic and represented using Fourier modes. The stratification and the wind forcing are taken to be horizontally uniform, capturing the forcing at a scale much larger than the mesoscale.
Smaller-scale structure in the wind stress can generate smaller-scale NIWs, but the energy input tends to be strongly dominated by the large-scale winds (Rama et al. 2022). To construct the mesoscale streamfunction used in the simulations, we take 𝜓 from observations and calculate the vorticity by taking the finite-difference Laplacian of 𝜓 on the sphere. We then interpolate this vorticity onto the Cartesian simulation grid centered on the location of the central mooring.
We apply a taper to the vorticity, such that it goes to zero on the domain boundaries. We invert this tapered vorticity field for the streamfunction on the periodic domain, making the resulting streamfunction periodic as well. Our conclusions are neither sensitive to the form nor width of the taper. For the results shown below, we use the following form of the taper:
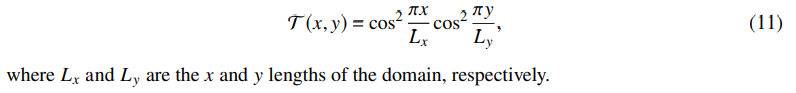


When the winds blow on the ocean surface, they generate turbulence that mixes momentum downwards. If a mixed layer already exists and is not too deep, the momentum input from the wind will be rapidly homogenized within the mixed layer (Pollard and Millard 1970; Kato and Phillips 1969). For some events at the OSMOSIS site, the mixed layer was up to a few hundred meters deep. These deep mixed layers are likely the result of convection driven by buoyancy forcing rather than the mechanical wind forcing (Thompson et al. 2016).
In these cases, it is unlikely that the momentum is uniform across the mixed layer, especially if the buoyancy forcing has ceased. The depth structure of NIWs obtained from the OSMOSIS mooring confirms this picture. The waves are initially forced over a layer that is thinner than the mixed layer before they propagate to depth.
To avoid forcing over an unrealistically large depth, we cap the forcing layer at 80 m. This value is guided by the observations and represents an average depth over which waves are forced when the mixed layer is deep. We discuss possible ways to improve this representation below.
In order to solve the YBJ equation, we must further specify vertical boundary conditions. The requirement that the vertical velocity is zero on the top and bottom of the domain translates to the requirement that 𝑀 be horizontally uniform at the top and bottom boundaries (Young and Ben Jelloul 1997). Since 𝑀 is determined by 𝜕𝑧𝑀 up to an arbitrary horizontal function, without loss of generality we specify 𝑀(𝑥, 𝑦,−𝐻,𝑡) = 0. The top boundary condition can be found by vertically integrating the YBJ equation twice and requiring that 𝑀 be horizontally uniform at 𝑧 = 0 (Appendix B). The result is
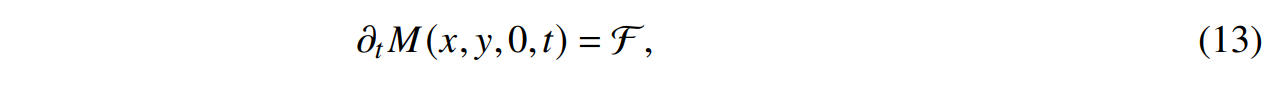
which we integrate a priori and then use as a Dirichlet boundary condition on 𝑀.
This paper is available on arxiv under CC 4.0 license.
